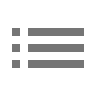본문

비행법칙의 기본에 대해 좋은 글이 올라와서 저도 가세해 봅니다.

‘페이스 앵글과 스윙궤적의 조합이 아홉가지 구질을 만들어낸다’는 사실만 제대로 이해하면 좋은 샷을 치는 덴 지장이 없습니다만, 사실은 그것이 D-plane 이론 자체인 건 아닙니다.

D-plane 이론은 벡터의 조합으로 이뤄진 간결한 수학적인 모델이고, 그 모델이 친숙해지면 3차원적 볼 비행원리 전반이 한꺼번에 직관적으로 이해되기 때문에, 혹시라도 조금 더 알고 싶으신 분들이 계시다면 도움이 될 수 있도록 교과서적인 엄밀한 정리를 써보려 합니다.

** 이름은 무슨 뜻?
D-plane은 임팩트 시 비행조건을 설명하는(descriptive) 평면plane 이라는 의미로 건조하게 지은 이름입니다. 물리학자 Theodore P. Jorgensen이 The Physics of Golf, 2nd Edition을 저술하면서 도입한 개념입니다.

** D-plane의 정의
교차하는 두 직선이 있으면 한 평면이 만들어지죠?
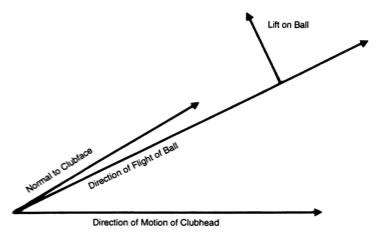
D-plane은 임팩트 시 1) 클럽헤드의 진행방향 직선과 2) 클럽페이스에 수직인 직선에 의해 결정되는 평면을 의미합니다.

이 평면은 지면에 대해 수직일 수도 있고 기울어져 있을 수도 있습니다.

D-plane 이론은 그 평면 상에 만들어지는 두 가지 벡터까지를 포함하는 이론입니다. 위 그림의 각 성분이 모두 들어가 있어야 D-plane 모델이라 할 수 있습니다.

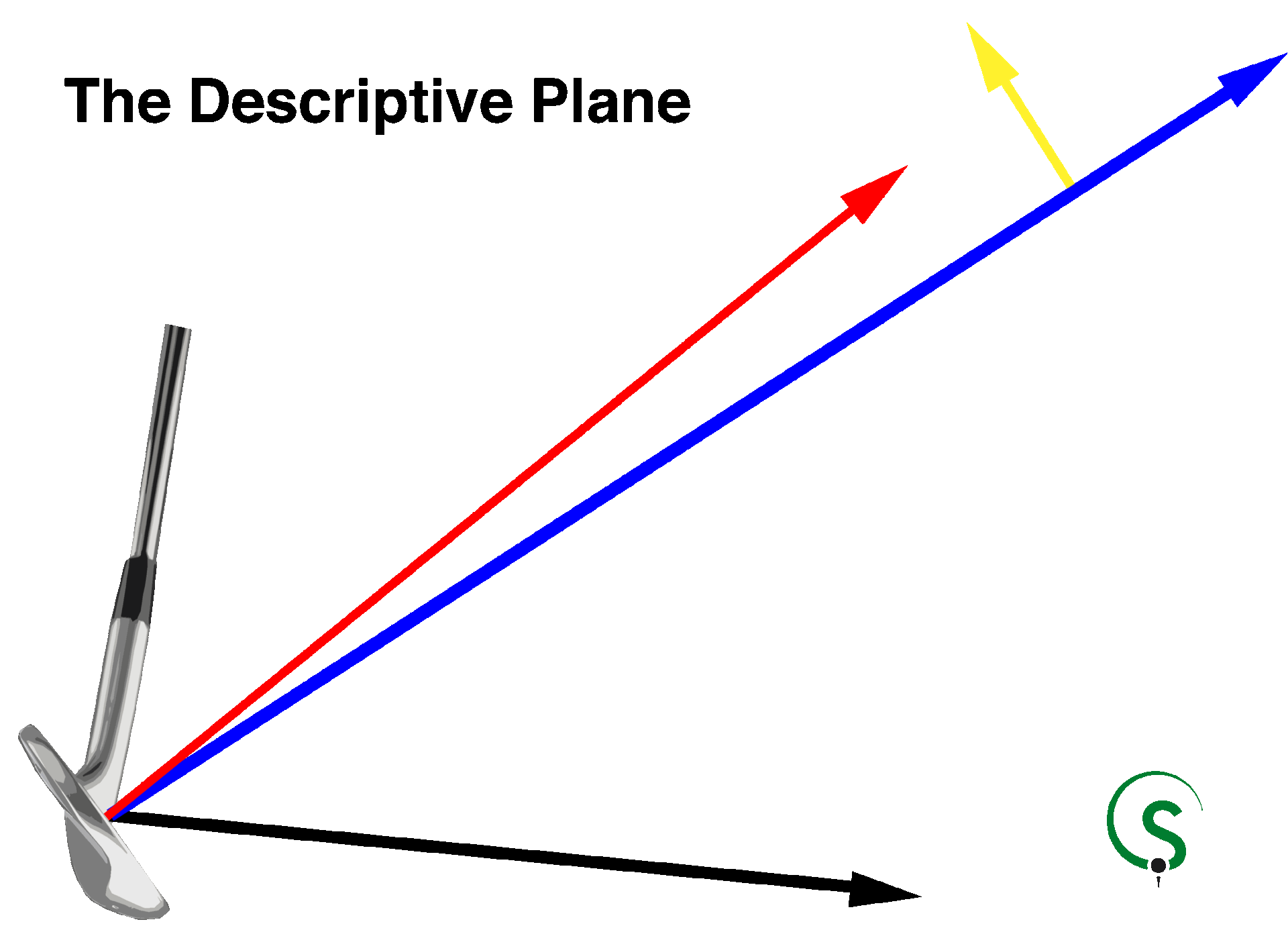
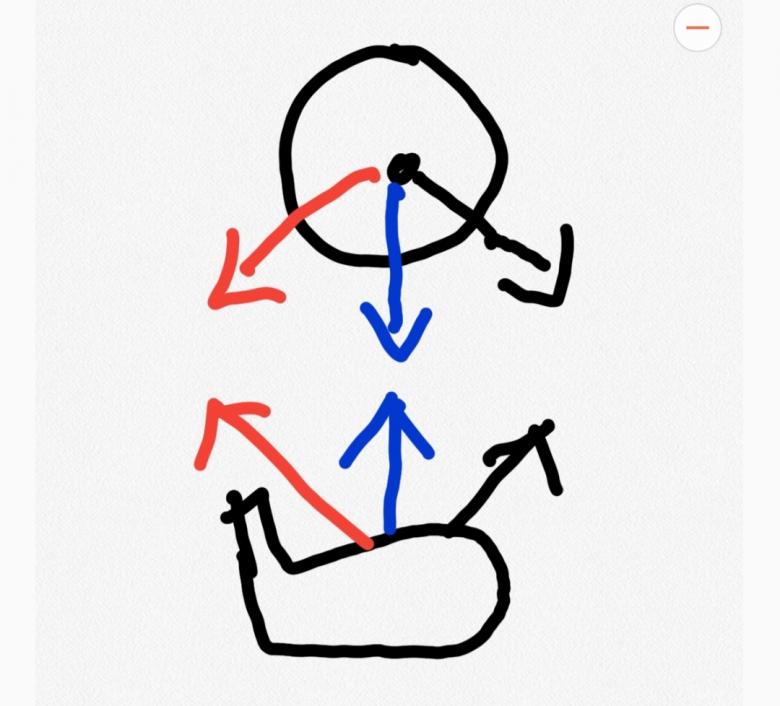
위 그림에서 핵심적인 두 벡터를 색깔로 구분한 것입니다. 파란색 화살표는 볼의 초기 발사방향이고, 노란색은 그에 수직인 양력lift 벡터입니다. 파란색 벡터는 페이스방향(빨간 화살표)에 훨씬 가깝지만 스윙궤적(검은 화살표)에도 약간 영향을 받습니다. 파란색 벡터의 크기가 클수록, 즉 볼스피드가 빠를수록 노란색 벡터도 커지고, 여기에 표현되지 않은 백스핀량이 클수록 노란색 벡터가 커집니다.

위에 언급했듯이 이 평면은 지면에 대해 수직일 수도 아닐 수도 있습니다. 따라서 노란색 화살표도 지면에 대해 비스듬히 기울어져 있을 수 있고, 그 때 훅이나 슬라이스가 발생하는 것입니다.

D-plane 이론은 결국 “볼 비행조건에 관련된 모든 방향과 크기 조건을 한 평면에 예쁘게 합쳐서 벡터조합으로 보여주는 수학적 모델”인 것이구나, 정도로 생각하시면 되겠습니다. 아홉가지 구질 다이어그램은 D-plane 이론이 아니라 거기서 도출된 결과물에 불과합니다.

** 3차원적으로 봅시다

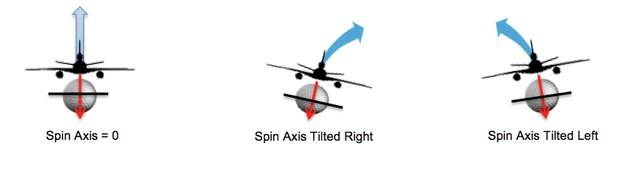
‘사이드스핀’이란 개념은 없고 스핀축이 단지 기울어진 것이다 라는 이야기를 들어보셨을 겁니다. 기울어진 스핀축을 수직/수평성분으로 나눠서 사이드스핀을 표현하는 덴 저는 딱히 불만이 없지만...아무튼 그 이야기를 떠올리며 D-plane과 함께 기울어진 스핀축을 비행기 날개라고 생각하고 보세요. 슬라이스 궤적으로 기울어져 날아가는 비행기가 직관적으로 상상됩니다.

** 명강의 영상
위에 언급한 내용에 덧붙여, 페이스방향과 스윙궤적의 차이를 스핀로프트라 한다는 사실만 기억하시면 자막 없이 눈으로만 보셔도 이해가 되실 것 같습니다.

** D-plane 이론이 아닌 것

이렇게 훌라후프를 이용해 하향타격/상향타격과 스윙궤적 인/아웃 관계를 설명하면서 D-plane이론에 대해 설명한다고 착각하는 교습가들이 제법 있습니다. 임팩트 근방의 스윙플레인이 D 모양이라 그런가? 이건 스윙플레인과 궤적 자체의 개념이지 D-plane 이론이 아닙니다.